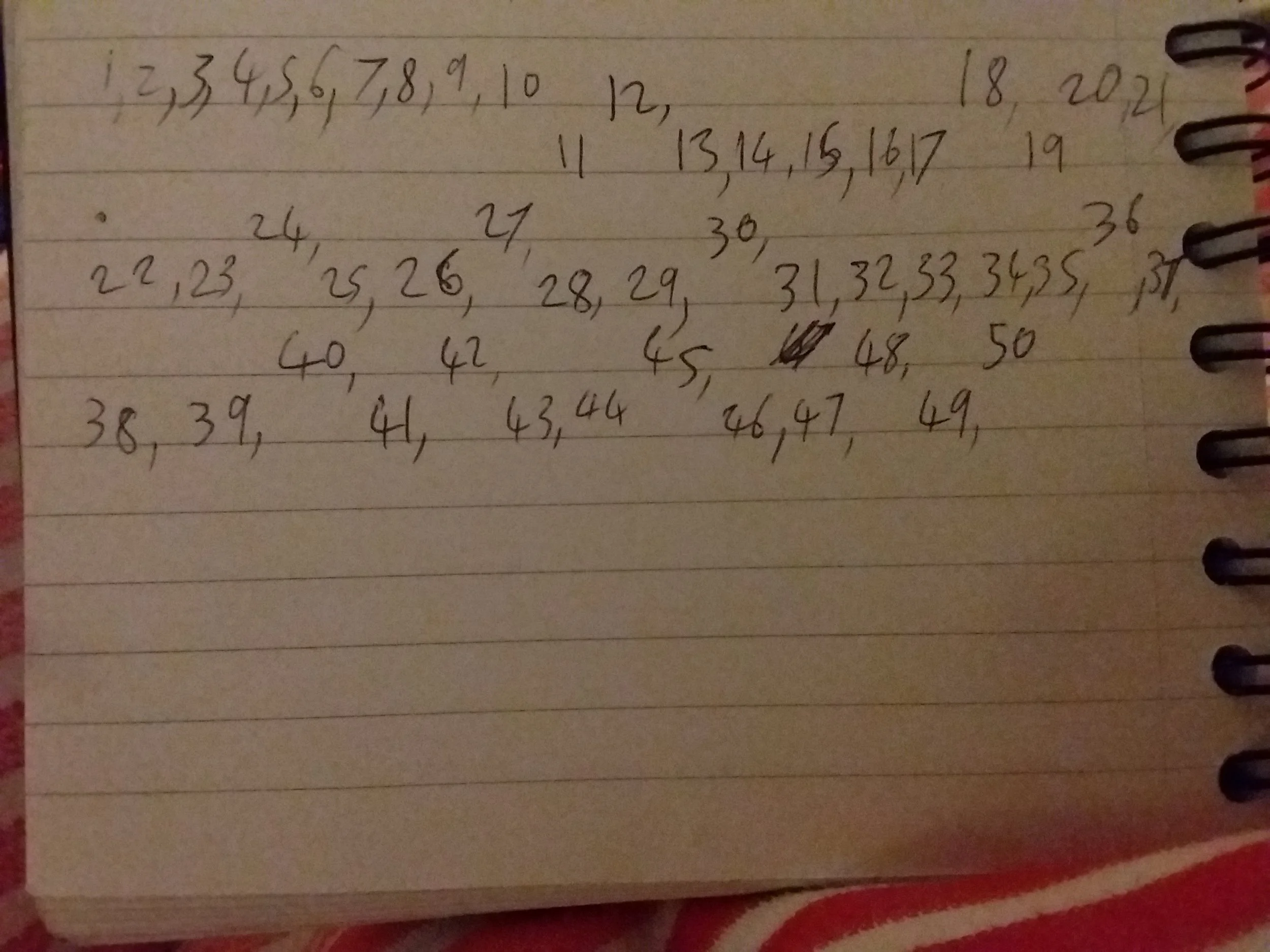Harshad Numbers

The digit sum of a number is the sum of its digits: for instance the digit sum of 18 is 1+8=9. Notice that in this case the original number is divisible by its digit sum; in this case 18/9=2. We call such numbers Harshad Numbers and they pop up in a couple of places across mathematics, including the concept that led me to them: self descriptive numbers (article on this coming soon).

If we look at some of the smaller numbers and analyse whether they are Harshad or not, immediately we see all the numbers 10 and below are. The one digit numbers have to be and the number of which we are in the base of will be no matter which base we are in. 11 is the first non Harshad number and it isn't hard to convince yourself that all primes larger than the base are similarly non Harshad.

Here's a picture of the first 50 numbers either raised for Harshad or dropped for not:

Notice that multiples of 10 and multiples of 9, both look like Harshard numbers in general, but neither statement is true. The multiples of 10 break down when you have multiple digits in front of the 0, so 130 is the first that breaks the pattern (although powers of 10 are safe). Multiples of 9 break down at 99.

One sequence of numbers that takes considerably longer to break away from being Harshad are the factorial, which by nature of having so many factors are usually in the pattern. Incredibly, the first to break rank is 432! which isn't. It has been proven that in base 10 you can never get 21 consecutive Harshad numbers but you can find an infinite number of 20 in a row (although this only occurs for the first time infeasibly far along the number line.

What may be some fun to explore are Harshad Numbers in other bases. For instance there are (only) four numbers which are Harshad in every number base and one further (12) which is only non Harshad in a single base, so leave it to you to find those numbers and that base.