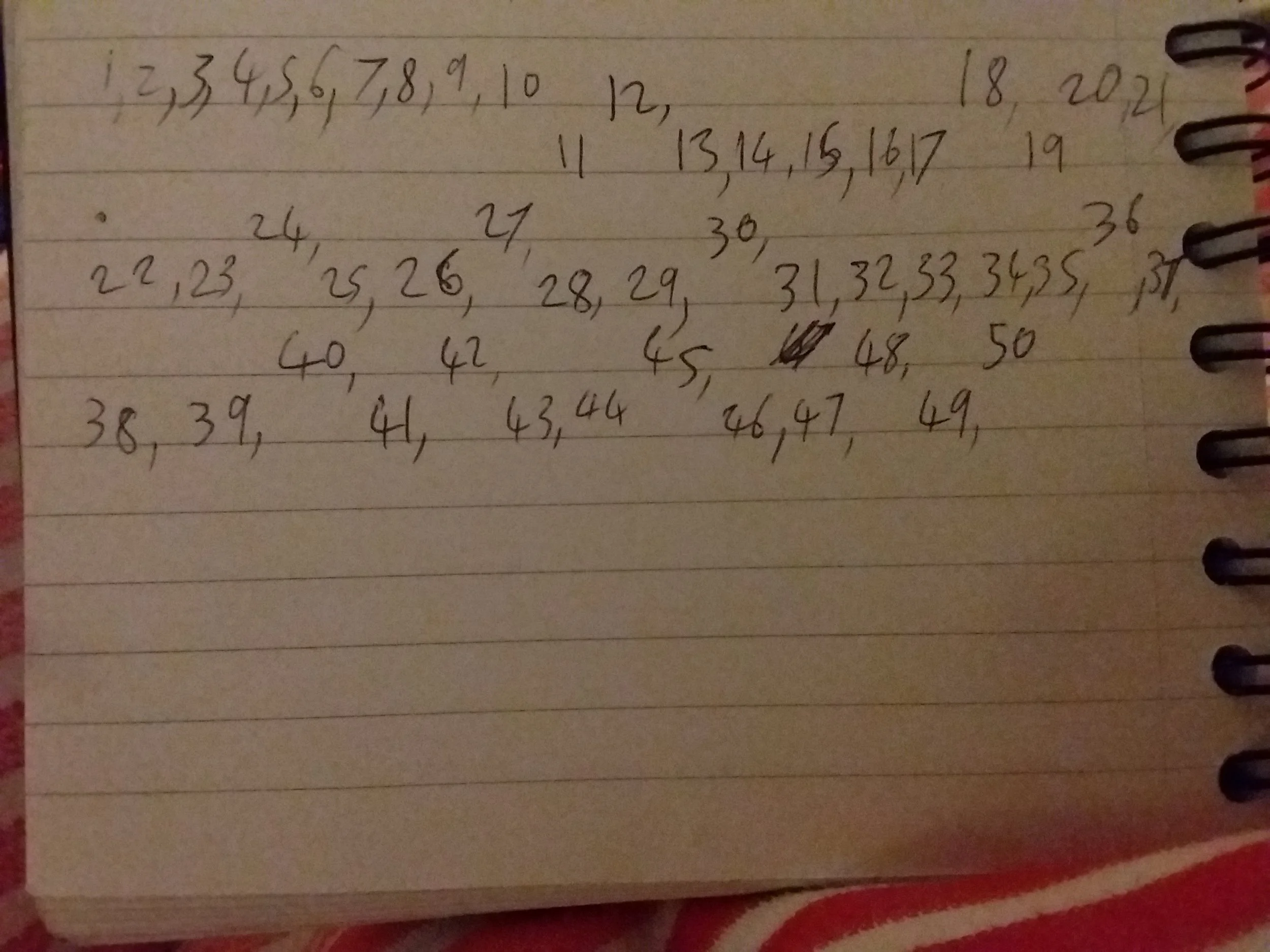Normal Numbers

A number is normal in base 10 (the number system that we use) if all of the digits 0-9 are all equally common in its decimal expansion. Also all two digit combinations 00-99 are equally common as each other. Also all three digit combinations 000-999 are equally common as each other etc.

For instance, if we look at the number 0.1234567891011121314... which is obtained by just concatenated all of the natural numbers, we find that it is normal in base 10.

Another less obvious example is 0.23571113171923... which comes from the primes, which was proven to be normal in base 10 by Erdős and Copeland in 1946.

However if we look at something like Root 2 or Pi we just don't know whether they are normal in base 10 or not. In fact, there are no numbers that we have found to be normal in base 10 except for those explicitly created for the purpose.

Now to expand the concept slightly, a number is normal if it is normal in every base. So if a number is normal in base 2, 3, 4... then it is normal overall. All of the numbers above appear to fail this prerequisite.

We have proven that almost all real numbers satisfy this stronger definition of normal. However we are yet to find a single number which is normal. Go and reread those last two sentences, there isn't a mistake.

Good work maths, you teasing enigma you.