Polygonal Number Last Digits

I want this article to be an extensive to one of the problems we analysed in Odds and Evenings episode 1. However you don't have to listen to episode to understand this. In the episode we had a think about the possible last digits of triangle numbers when you write them out normally (base 10). We came to the conclusion that the last digits from 0-9 occurred with the frequencies 4, 4, 0, 2, 0, 4, 4, 0, 2, and 0 within the first 20 triangle numbers and then they got caught in a loop where they repeated thereafter. So, no triangle number will ever end in a 2, a 4, a 7 or a 9, and the relative frequencies of the other last digits remain in the same ratio forever.

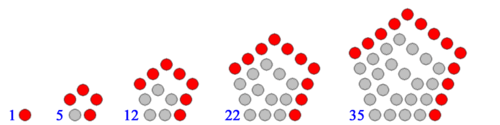
After the episode I got thinking about other sequences of numbers and I thought I would investigate other polygonal numbers. So instead of triangle numbers I would take the square numbers, the pentagon numbers and so on. You may not be familiar with the pentagon numbers and higher, but they are exactly the same in spirit to the triangles and the squares like so: 

The squares are easier to analyse than the triangles on two counts: firstly people tend to be more familiar with them and secondly the pattern repeats after only 10 because it is only the last digit of the number before squaring it that affects the last digit of the square. The last digits go 1, 4, 9, 6, 5, 6, 9, 4, 1, 0 before repeated. Once again we can enumerate these and pop them in a table:

Both of these patterns repeat after every 5, which as far as I can tell will always be true. There is twofold symmetry in these problems because counting up or counting down should give you the same pattern. Let's see what we get with the pentagonal numbers:

We are back up to a period of 20. This gives us the hypothosis that maybe the shapes with an odd number of sides have a period of 20, while those with an even number of sides have a period of 10. It makes sense to just try a few more before we do a proof.

I've honestly never knowingly spotted a mistake on wikipedia before. 

So the period pattern does continue for the next couple. Since there is a generating formula for the nth term of polygonal numbers that seems a sensible place to start. For sides S, the nth polygonal number is P(S,n)=(n^2(S-2)-n(S-4))/2. For S even and S odd we can simplify the formula and try sticking in n as 10 to see what happens.

This looks fairly conclusive and it is easy to check that popping 20 into the odd case will always give a multiple of 10, so no polygonal number series is going to have a larger period than 20.