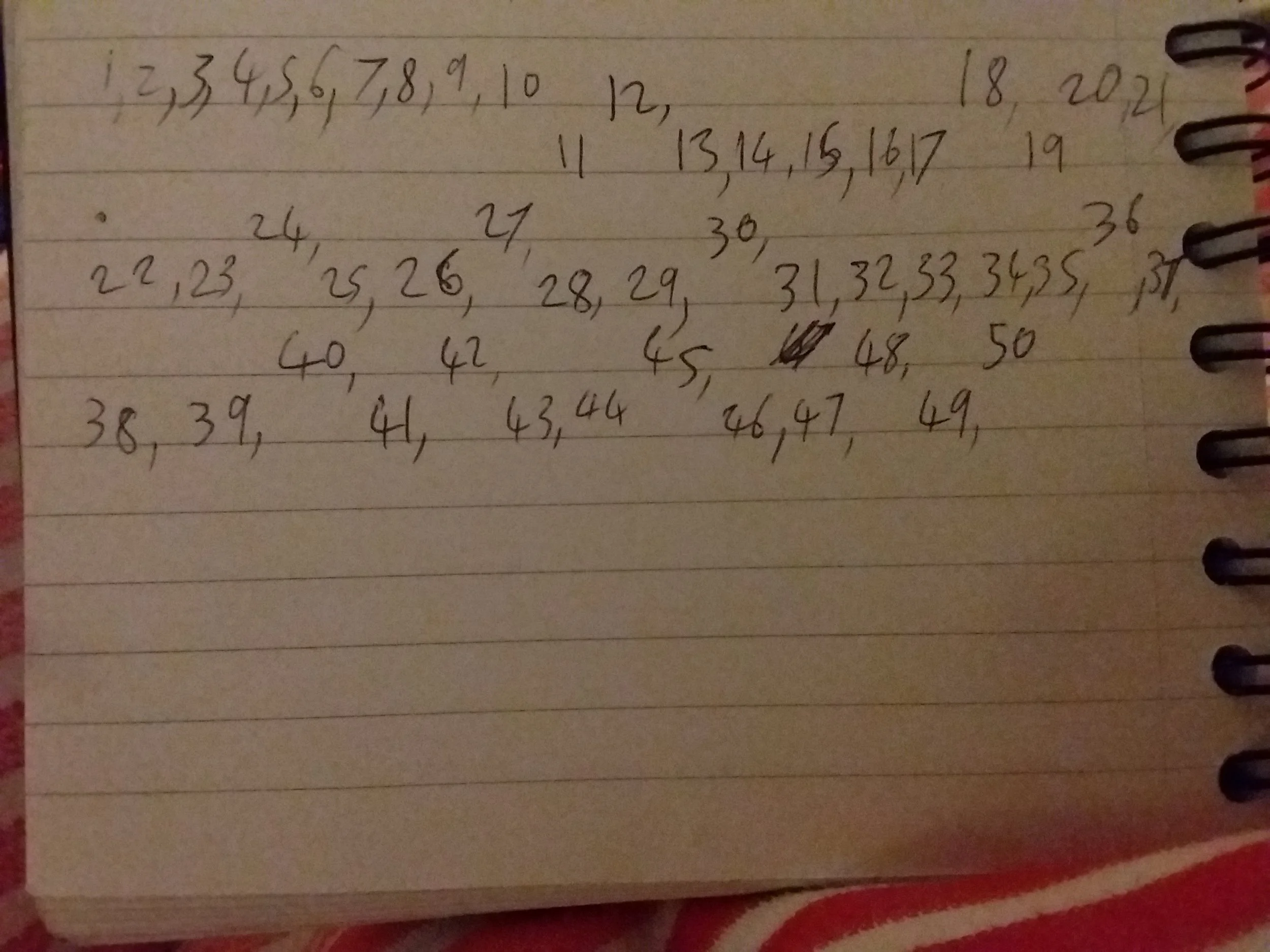Intersecting Lines
Here’s a pleasing question from the UK Maths Challenge today. There are a collection of lines in a plane such that each line has exactly 10 intersections. Which of the following are not a possible number of lines which could have this property?
11
12
15
16
20?
Have a go and join me for discussion of the general problem below.
…
The answer is D. 11 is the easiest to see with by having them all have different gradients so that every one of them will intersect with all of the others. Notice that that is the smallest number of lines that we can use. At the other end of the spectrum we can have 20 lines by having two sets of 10 parallel lines, so each line intersects only with the 10 lines in the other set.
This is what gave me the idea for it more generally. By having groups of parallel lines we can fit more total lines in. If we attempt to have clumps of lines with different sizes then we get some lines with different numbers of intersections which we want to avoid, because we want all of them to have exactly 10 intersections.
So our options are clumps of 1, 2, 5 or 10. 1,1,1,1,1,1,1,1,1,1,1 or 2,2,2,2,2,2 or 5,5,5, or 10,10. Each of these has one extra group to actually do the intersections with, so we end up with 11, 12, 15 or 20. Thinking about it as 10+1, 10+2, 10+5 or 10+10, so 10 plus each of its factors.
Doing this more generally, to find the acceptable number of lines which each have n intersections for different values of n, we get the following table:
The number of possible ways is just the number of factors of the number of intersections you are after.