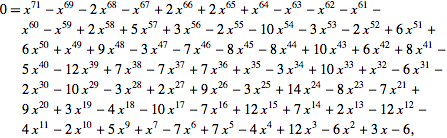Help Needed on a Puzzle

I was doing a functional skills maths paper where they had to fit 8 L tetraminoes onto a 6x6 grid in some way. Here is one possible solution:

It got me thinking: could you fit in 9? The solution above leaves 4 empty spots, but they are arranged in a 2x2 square. I've tried lots of different attempts and I've managed to get the 4 remaining dots to form a square, a straight line, a curvy piece (the ones that you don't want from Tetris) and various disconnected designs, but I can't make them form the space needed for another L. Feel free to flip the pieces as you like, but can you fit 9 in? Alternatively can you prove that it is impossible? I'd like an Aha! moment of insight to see why it is impossible, but brute force may have to be the way.

An example of an Aha! sort of proof would be proving why the remaining four spots will never form a T tetramino after you have fit in 8 L’s. If you imagine colouring in the 6x6 grid as a checkerboard then there would be 18 black squares and 18 white squares. Each of the L tetraminoes would cover exactly 2 white and 2 black squares. However the T tetramino would either cover 3 black and a white, or 3 white and a black, so we have a parity issue. For a similar style of problem see this video:

So, an appeal for help on this problem. If you have any success with the proof (or can find a way of fitting in the 9 L’s) then tell me about it on abt@hereford.ac.uk

Thinking about it slightly further, 2x2 is impossible, 4x4 is possible, 6x6 is unclear, but 8x8 can just be done by using 4 4x4 solutions put together. This works for anything of the form (4m)x(4m). Can we come up with a general solution to which grids are possible and which are not?