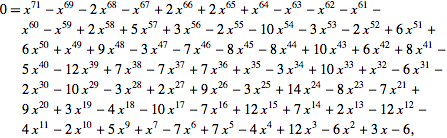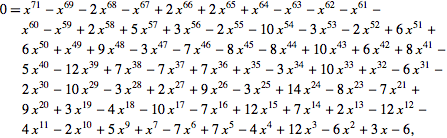1, 11, 21, 1211...

Here's a classic puzzle. What's the next in the sequence?

1

11

21

1211

111221

312211

13112221

1113213211

…

Hint, try reading it out loud.

….

This is called the Look and Say Sequence. The first line (1) has one one. The second line (11) has two ones. The third (21) has one two and one one. Each one is describing the number before it.Q

Looking for patterns in this sequence yields a few results. Firstly the last digit will always be 1 and the penultimate will forever alternate between the values of 1 and 2. However the rest of the numbers appear more chaotic. Apart from noticing that they consist of lots of small digits (1, 2 and 3) and that they grow in length, it is hard to get anything else.

This suggests two problems to investigate: will any digits higher than 3 occur and will the number get longer forever? By starting with different numbers on the first line there is also a lot to explore. For instance the number 22 is invariant under the operation and is the only such number although this is far from obvious. This is actually the only starting seed that doesn't grow indefinitely. The only time you will get a number higher than 3 is if you start with one (as in a number greater than 3) or if your initial seed has a sequence of more than 3 of the same number in a row.

The limit of the ratio of the length of each number compared with the previous one is 1.303…, i.e. they get slightly over 30% longer each time. This is true for all seeds that aren't 22. John Conway calculated that this ratio is an irrational number which is exactly the only root of the polynomial: