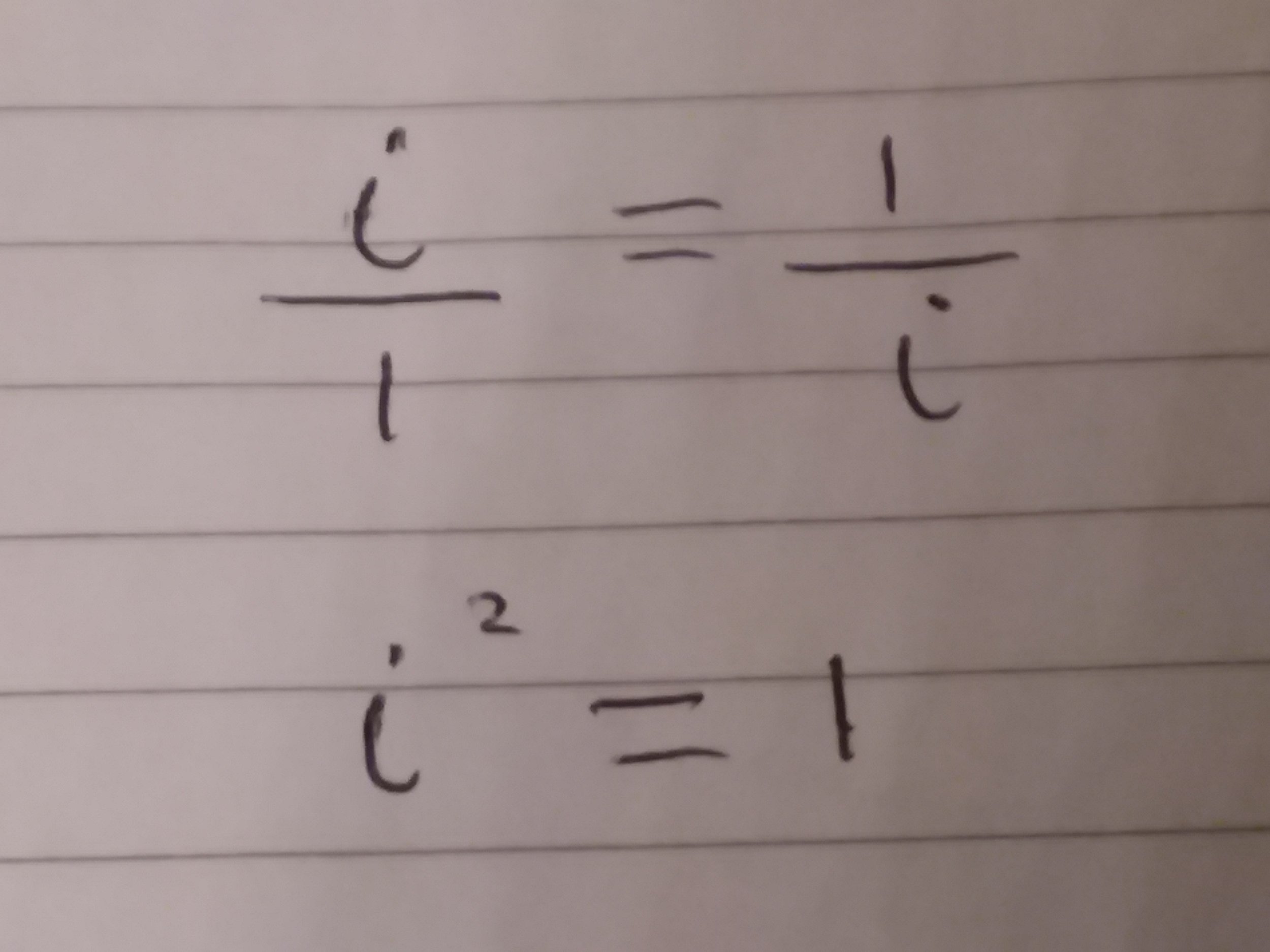A Complex Trick
OK here is a classic trick that involves complex numbers. If you haven't met them yet then all you need to know is that the square root of negative one can't be done with real numbers. After all, if we square a number it will be positive. But we can define a square root of -1 to be some imaginary number i and see what happens. Normally it is completely consistent and it is used all over mathematics and science, but it can get you into trouble if you are not careful.
Before we start, realise that if we square both sides of i=sqrt(-1) we get:
OK, I'm going to start with a completely innocent identity and work myself down to something which clearly isn't true. If you have seen one of those false proofs that 0=1 then you know the format: try to find my mistake in logic.
No tricks yet, you can verify that both sides are indeed equal.
To get from one line to the next we can take the square root. You are correct to be wary of the lack of plus-minus's here, but it really is fine; I'm simply taking the positive root of each side to be equal.
Applying surd rules I am splitting the square roots into two. If unconvinced, try writing everything to the power of a half instead and use indices rules and you will get the same thing.
By definition the square root of -1 is i and the square root of 1 is 1.
Crossmultiplying, I've multiplied up by i and by 1 to get a result.
So we had i^2=1, but by defintion i^2=-1, so -1=1? Something is clearly wrong here.
So where did it go wrong? Scan back and see if you can convince yourself of which point the equality no longer holds. I'll reveal below.
...
OK so the trick happens when you split the surds. What would normally be completely true with real (none imaginary) numbers no longer holds. Unlike the classic 0=1 tricks that all rely on dividing by 0 subtly, I wasn't aware of this one until I did teacher training and another teacher in waiting showed this to me. I love it, it made me question whether I actually understood complex numbers and indices at their core.