Due South, Due East, Due North

There is a classic puzzle that a lot of people encounter at some point during primary or secondary school. A bear walks 10 miles due South, then it walks 10 miles due East before finally heading due North for another 10 miles. It finds itself exactly where is started. What colour is the bear?

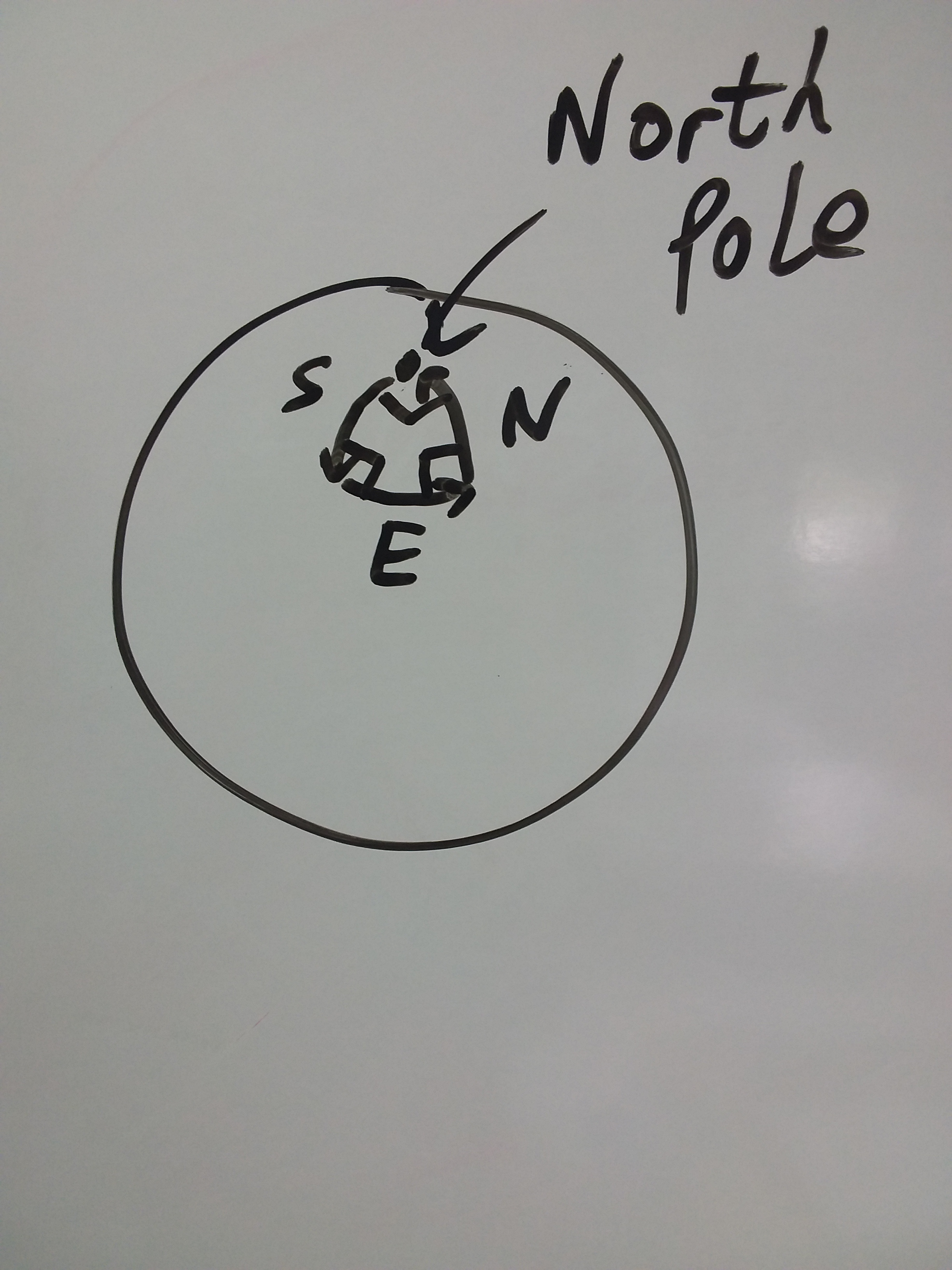
Of course, what we are looking for here is a place on the Earth where this is possible. On the face of it, it appears that we are travelling three out of the four sides of a rectangle; but that isn't quite true. Imagine if you started at the Geographical North Pole (see this earlier article for a pedantic look at the different types of Pole). Any direction you head in will be South, so you walk to 10 miles. Next you turn to go East and you travel 10 miles around the curve of the Earth, until you turn to go North again. Since you had previously traveled 10 miles from the Pole, you will have the same distance to go back again. Therefore, the answer to our question is white. (Interesting side note, Polar Bears have black skin, but we'll assume that the bear in our question hasn't been shaved.)

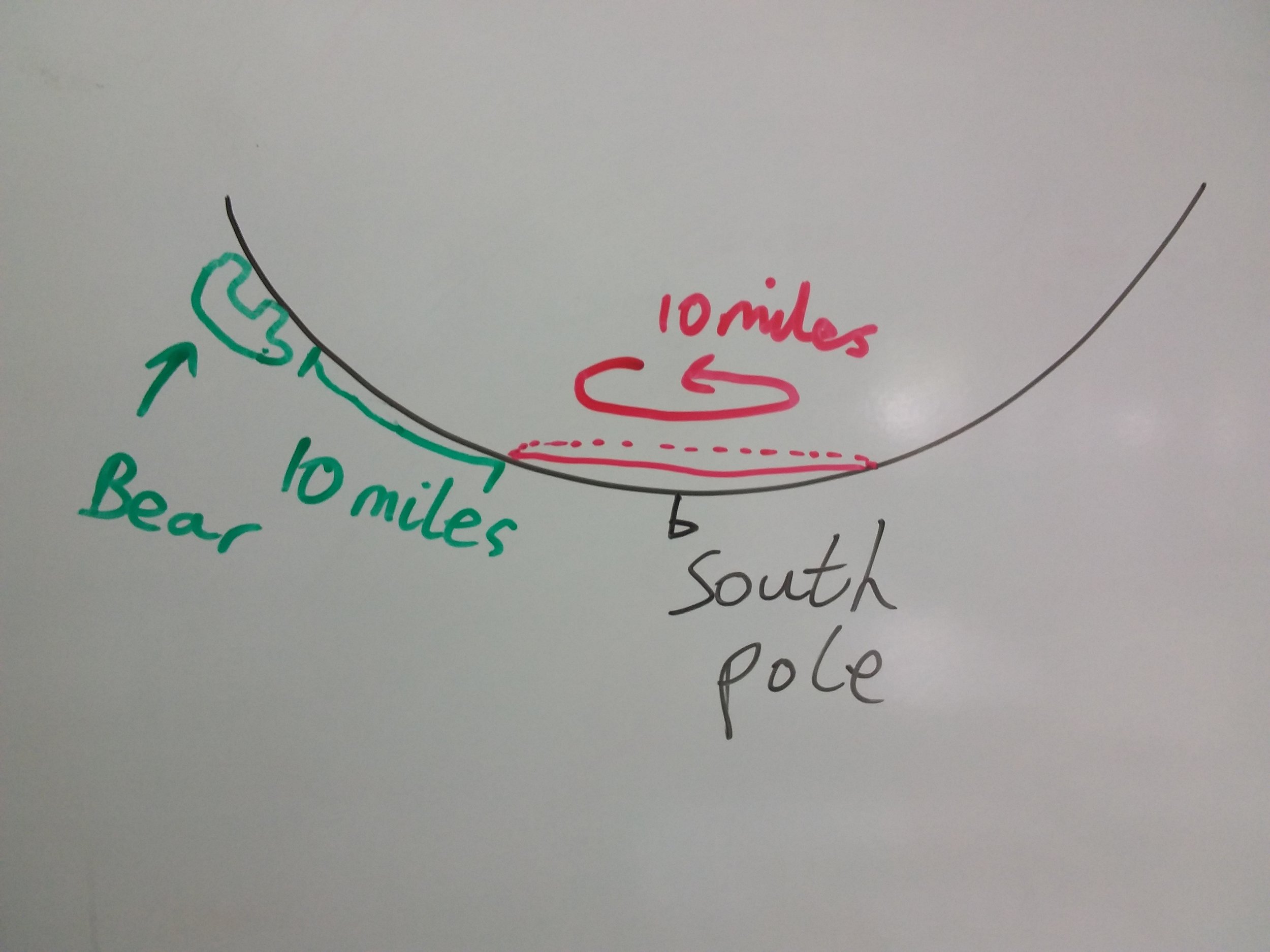
However, this isn't the only place on the Earth that will satisfy our geography problem. On the picture below our plan is to find the place on the Earth where walking 10 miles due East would complete one revolution (in red). So by starting at any point 10 miles North of this ring we could go South (in green), do a circuit of the Earth (in red) and then head North to return to where we started (green again).

Where exactly is this ring? Well the radius of the Earth near the South Pole is 7900 miles (it isn't constant, see here for detail). The ring ends up being 7900arcsin(5/(7900Pi)) (in radians) which is approximately 1.59 miles from the Pole. Thus the bear should start 10+1.59 miles from the South Pole.

But we can adapt this method to find a family of solutions. By starting in closer to the South Pole we could have our 10 miles walk to the East cicumnavigate the Earth any integer number of times and still end up back where we started. This rings get tighter and tighter around the South Pole and there are an infinite number of them. The formula for them is 7900arcsin(5/(7900Pi*n)) where n is the number of rotations. This gives 0.80 for n=2 and can roughly be modelled as linear since arcsin(x) is approximately equal to x for small x.

So why aren't these acceptable answers to our original problem? All of these solutions fall within Antarctica, so there are no bears of any colour.