A Topology Problem

The field of topology deals with the intrinsic properties of shapes without worrying about their size. You can think of the objects as infinitely stretchy and moldable, but as you manipulate them you are prohibited from tearing the shapes. Below is a gif showing the idea with a torus being manipulated into a mug. They both have one hole and all of the movements are continuous.

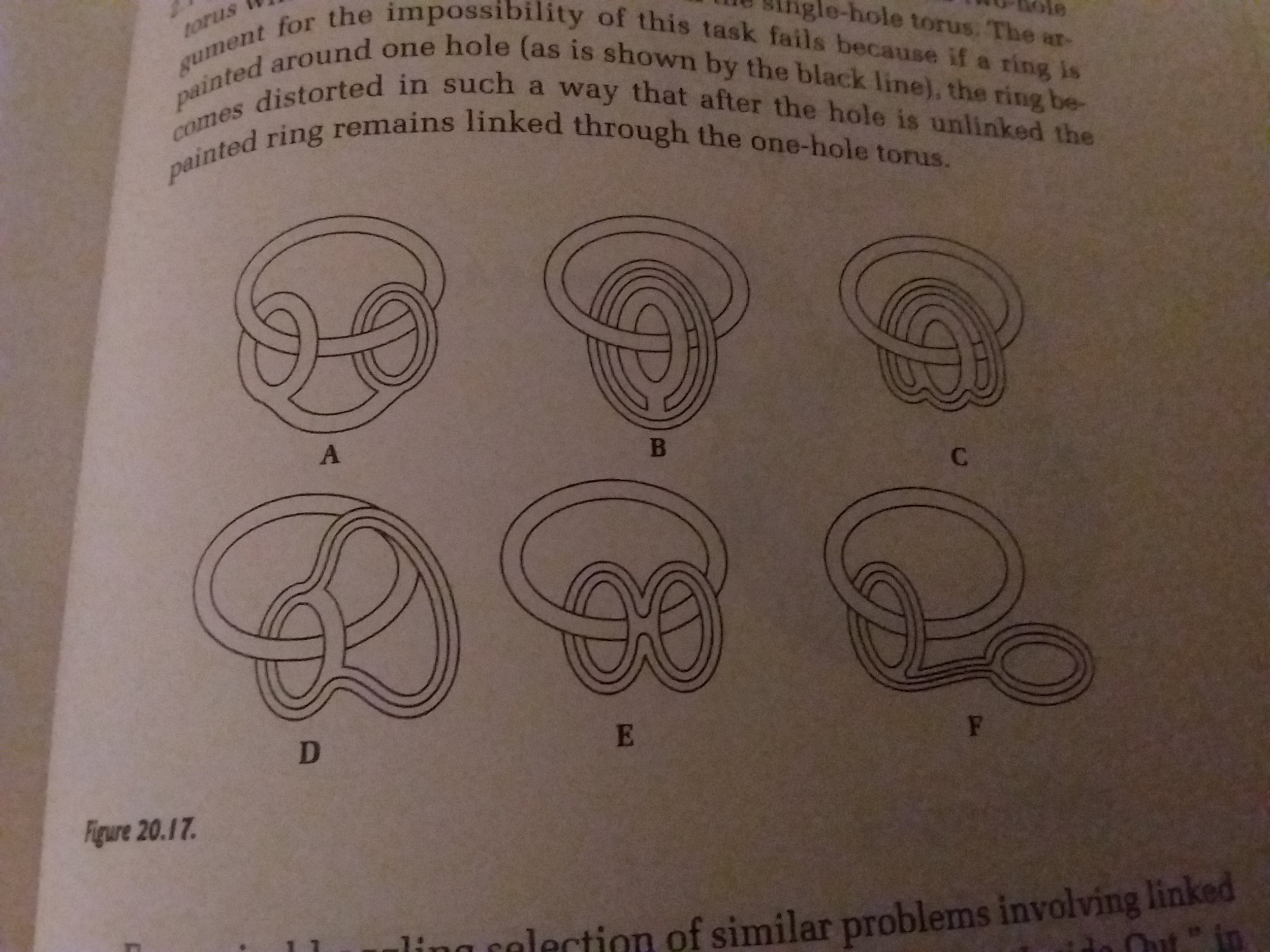
With the rules set I present a problem from a column in Scientific American by the ever brilliant Martin Gardner. The two shapes below have similarities, but if you look at the black rings that have been drawn on the surface of each there is an apparent problem. There is no way to manipulate two unconnected rings to make them linked like a chain without cutting one of them. e.g. if you had two elastic bands you couldn't link them without breaking them. So it follows that the two shapes can't be manipulated into one another. Doesn’t it?

Explanation below.

Here's a picture of Gardner’s solution:

This is one of those pictures that rather talks for itself. It is a deeply surprising result.