Braess' Paradox

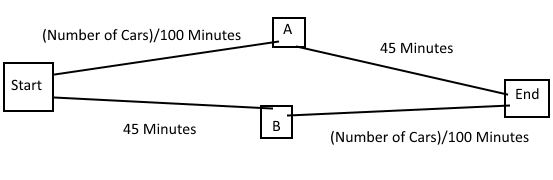
Here's a paradox from network theory. Imagine we have cars trying to choose the quickest route to get from the start to the end on the diagram below. They have two routes to choose from, going through towns A or B. The time taken for each road is either fixed or variable. The idea is that if a lot of cars try to use the same road then it gets congested.

Let's say we have 4000 cars making the journey. If 2000 go for each route then the journey will take 2000/100 + 45 = 20 + 45 = 65 minutes. If it didn't split equally like this then the journey time will only go up, so if everyone acts in their own best interest then this equilibrium will be maintained.

Now let's change the situation by building a new road between the towns A and B. They are very close together so the road takes close to 0 minutes of travel time as shown below:

This time the first decision for each car is to take a straight 45 minutes or a worst case scenario of 4000/100 = 40 minutes to get to A or B. It is in everyone's best interest to take the 40 minute route. The same applies for the second leg of the trip. This gives an overall journey time of 80 minutes, which is worse than before.

Thus we have an apparent paradox: by adding a road we have actually made the network worse. Obviously the numbers are a little cooked in this example, but on more complicated road networks this is an actual problem that city planners think about.