2d6 or d4+d8

Last night I was at a table top rpg night and I got thinking about dice. Typically games such as Dungeons and Dragons use platonic solids for most of their dice (apart from those with 10 faces which aren't platonic because they have irregular kites as their faces) which look like this:

We tend to refer to them with names such as d6 to mean a die with 6 faces. So usually we play with a set of d4, d6, d8, 2 d10s, d12 and d20. The reason we often have 2 d10s is so that you can make percentages by taking one die to be the units and the other to be the tens. Typically your character will have a certain amount of strength which corresponds to one die and your weapon will add in another die for your total attack. I've been thinking about what would be better out of the total result from a d4 added to a d8 compared with two d6s added together.

One of our modes of analysis is by considering their expected value separately. A d4 can roll a 1, 2, 3 or 4. This sums to 10 and so has an average of 2.5. Similarly the expected value for a d6 is 3.5 and a d8 is 4.5.

This means for a d4+d8 we have an expected value of 7: which is the same as 2d6. But let's look at the distributions. For 2d6 I think most people will be familiar with the table below: only a 1 in 36 chance of getting a 2 or a 12, but with a 6 in 36 chance of getting a 7. It is very bell shaped. 

However this table will probably be new. While there is still a trailing off at each, most outcomes have an equal spread of 4 out of 32 in the centre. If you can benefit from having lots of middling rolls with consistency then this might be better for you.

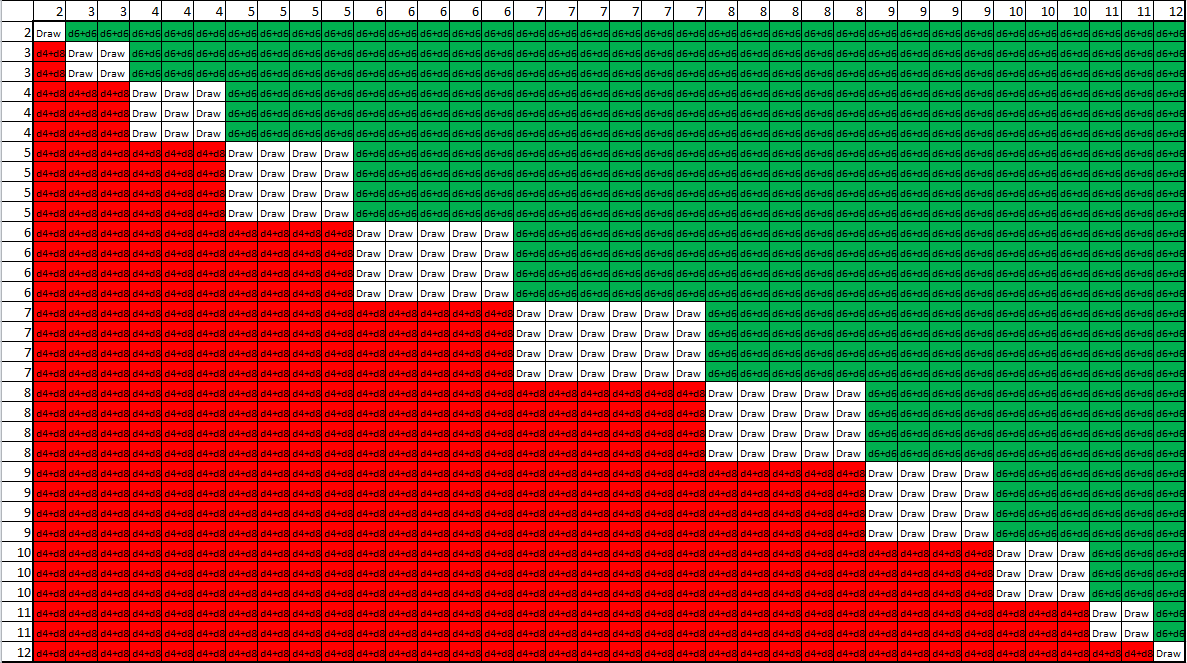
If you compared the total from the d4 and d8 and compared it with the 2d6 then the graph below would show you which is higher. The former is down the side while the d6s are along the top. I've colour coded the result with red being a d4+d8 win:

I'm not sure if the high degree of symmetry is shocking to you, but it was to me. There are 514 red cells and 514 green cells even though the distribution is slight different. So the conclusion we can draw is that it is only the variance which is affected.

Update: One of my students created a program to run through the numbers with other dice. d2+d10 also gives an equal chance against d6+d6. It looks like we have an invariant.