Magic Colours and Polynomial Roots

I was thinking about a related problem from FP1 earlier when doing the roots of polynomial equations. If you have a general quadratic in the form ax^2+bx+c=0 with roots α and β then you can form some identities related to the sum and the product of the roots. Similarly we can extend the pattern for higher order polynomials. Here's a picture which illustrates what happens when you start a diagram with a pen that doesn't have much ink left: 

In red I've enumerated what happens for each case. These are the rows of Pascal's triangle representing (on the quartic) 4C1, 4C2, 4C3 and 4C4. The missing 4C0 at the start would be 1 and that is the number of ways of picking the sum of 0 of the roots.

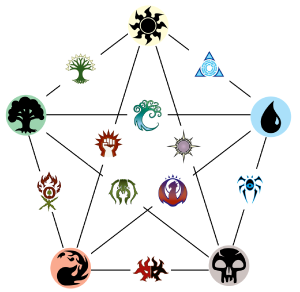
All of this reminded me of the same pattern that comes in deck building in Magic the Gathering. The five colours are White, blUe, Black, Red and Green (we use the letter U for blue because B and L are claimed by Black). Most decks in the current meta use two of the five colours of magic which leads to 10 colour combinations, each of which has a name. Since the colour wheel in Magic is presented as a five pointed star you can think of them as the 5 colour pairs around the edge: Azorius WU, Dimir UB, Rakdos BR, Gruul RG and Selesnya GW, plus the 5 enemy pairs going through the middle Orzhov WB, Izzet UR, Golgari BG, Boros RW and Simic GU. (I'm doing well at writing this from memory which lets you into how much time I spend reading about MTG on reddit.) 

So we have 5 single colour combos and 10 double colours. However in some sets there is support for 3 colour decks. About 2 years ago a set came out with wedges, which is the name for two colours that are next to each other on the colour wheel plus their common enemy colour. So, Abzan WBG, Jeskai URW, Sultai BGU, Mardu RWB and Temur GUR. To compliment wedges we have the shards (which haven't been prominent in a while in MTG) which are three colours next to each other on the wheel Bant GWU, Esper WUB, Grixis UBR, Jund BRG and Naya RGW. In total these make 10 3 colour combinations.

The four colour combinations are much rarer and don't have well agreed upon names, but there are five because there is one for each colour that could be missing. Finally there is only one five deck. Just like with the polynomial roots, if you wish to get the first 1 of the Pascal's triangle row then you can consider that there is one way to do a deck with no colours. In all we have 1, 5, 10, 10, 5 and 1 combinations of 0, 1, 2, 3, 4 and 5 colours. If magic did introduce another colour then we just get the next row down for 1, 6, 15, 20, 15, 6, 1.

I like it when the same structure of mathematics raises its head in different problems. Being able to use the language and logic you have built up in one context is often portable into the new setting which helps build insight. For me this week however it means I keep wanting to use MTG terms with my further maths class, but I know it wouldn't help.