God's Number — alaricstephen.com

God's Number is a rather grandiose term for the maximum number of moves it can take to reach any possible position on a Rubik's Cube. There are two ways of defining it because there are two ways of counting moves on a cube. The Quarter Turn Metric (QTM) counts every 90 degree turn as a move, while the Half Turn Metric (HTM) allows you the additional freedom to turn a side 180 degrees and still count it as one turn. As of 2014 both of these God Numbers have been proven to be fixed, at 26 and 20 respectively.

To get a lower bound you can count how many different positions you could reach in n moves at most. There are 6 faces, each of which can be turned in 2 directions which makes 12 different quarter moves in each position. So after 1 move you can reach 12 positions and after 2 moves you can reach at most 144 (although this is only an upper bound because some positions will be repeated at this stage). The number of different positions a cube can take is 43,252,003,274,489,859,856,000 which we can work out how many powers of 12 it would take to get up to this by using logs. Log base 12 of 43,252,003,274,489,859,856,000 = 18.1... so it will take at least 19 moves.

Allowing half turn moves you get an additional move per face which means there are 18 possible moves in each position. Doing the same work with logs we get a lower bound of 16 moves for HTM.

In 1995 we found better lower bounds by noting that there was one particular position that was very hard to get to, the so called superflip which requires at least 24 quarter turns:

All the edge pieces have been turned around.

Three years later we found a single position which required 26 moves; a superflip with 4 of the centres also swapped with their opposite number. It should be noted that these positions are outliers and almost every random position can be done in far fewer moves.

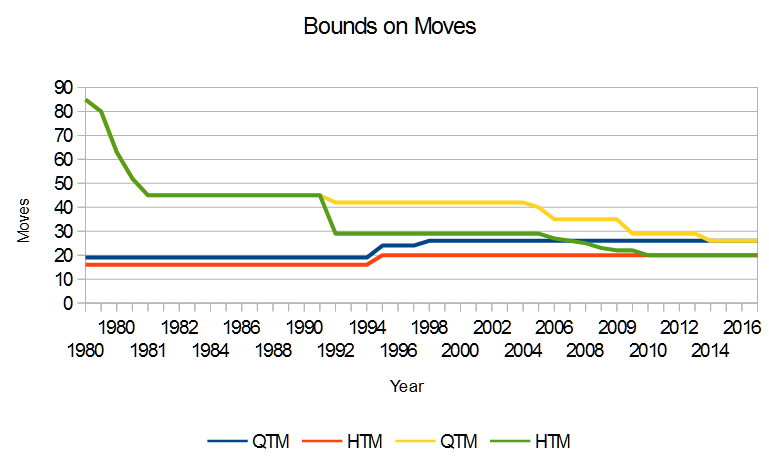
The work to find an upper bound has had a lot more steps in it. The first upper bound was 277 moves by just taking the worst case scenario at each step of a basic method. However, this was quickly improved up by John Conway among others until they hit a brick wall at 94 moves in 1979. The next year work by Thistlethwait in group theory lowered the bound down to 45 by the end of the year and his record stood until 1992 when another group theorist called Reid lowered it to 29 for HTM using a similar approach. These ever decreasing bounds were homing in on the God's Number for each metric from below and above.

Finally throughout the 2000s the upper bound on both metrics have been lower until in 2010 the HTM was fixed at 20 and relatively recently in 2014 the QTM was fixed at 26. Now that the lower and upper bounds are the same we can be sure we have our results.

Here's a graph I made of the bounds for both metrics over time: