GCHQ Resistor Puzzle Solution

I've spent the last day doing this GCHQ puzzle. I waited until I got to work on Monday so my students could help me with an issue I was having yesterday.

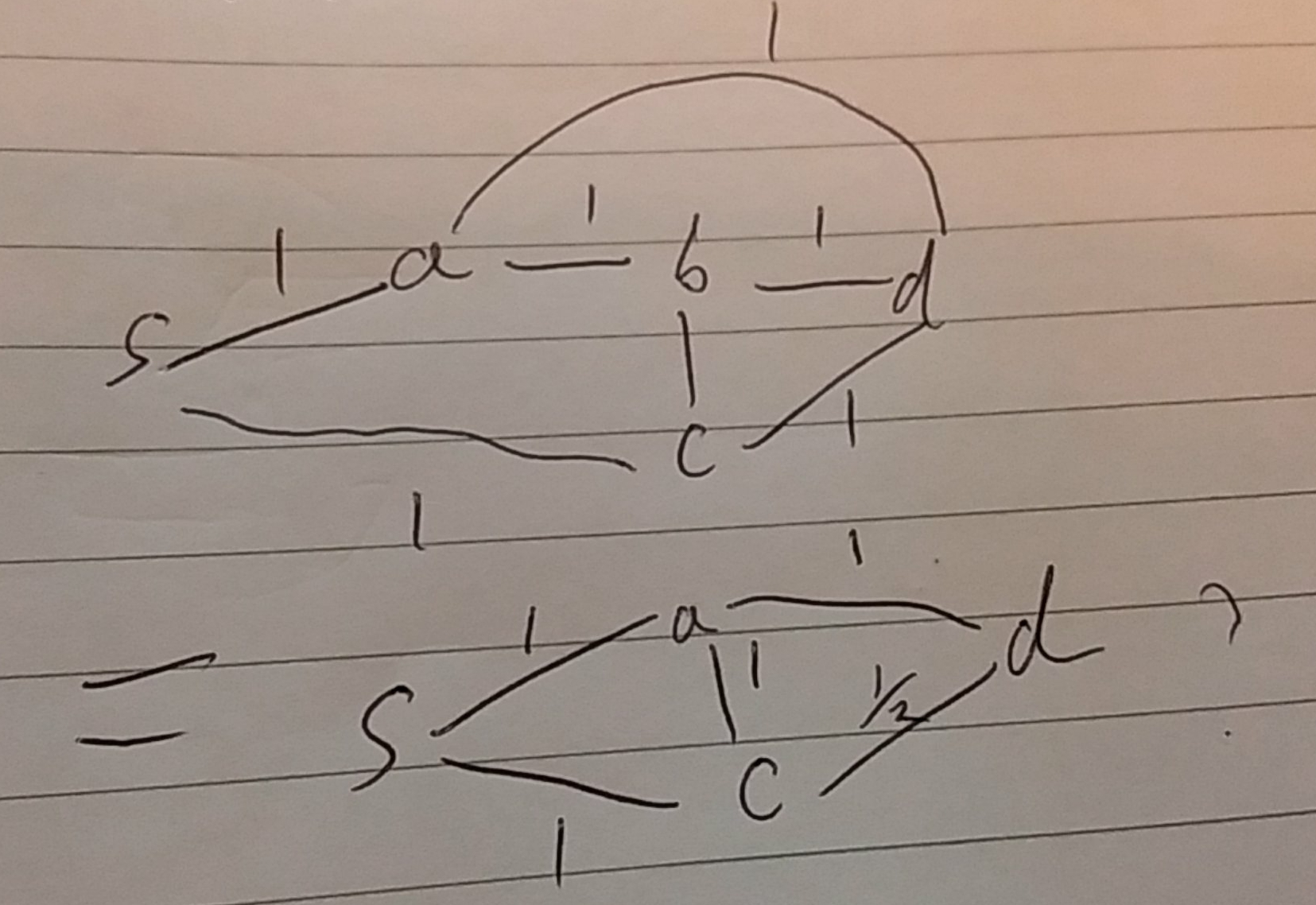
The Problem I had yesterday was with the third cluster to the left of the cell:

Drawing it out I reduced it a bit by combining two of the nodes to this:

At this point this second diagram illustrated the minimum case of networks that I didn't know how to solve. After going down a dead end of looking at a similar configuration called a Wheatstone Bridge, but I then found out about something called a Δ-Y transformation which can turn a triangle into a Y shape.

This turns our problem into one we can reduce using the normal series and parallel arguments. In fact it looks like being able to switch back and forth between Δ and Y, plus reduce the parallel and series resistors are universal: by which we mean we can solve any system. I haven't proved this yet but I'm going to have a think about it.

In general if I have a problem of the form:

This is hideous, but once we had this formula we were able to plug in numbers for any of that form. Since we had a class of people we split up the resistor clumps and crowd sourced the solution. Here are some photos of the process:

The smartboard held the numbering and as people resolved the clusters we slowly filled in the blanks on the board below.

We made lots of mistakes along the way, but two messages are forming. One reading down and the other up. As we saw words appear it gave us checks.

Hard at work.

Our final result. Notice the many fonts and ink colours from different people.

The two messages say: "Puzzled? Try looking at the unused letters" and "ever wondered what a puzzler does all day?" Crossing out the unused letters we get the remaining letters below:

Ignore the green highlighting. The y on the top line is not crossed out but the circled e is. Sorry :P

These lettrs give: Rvxdpxorhaxepzzoamxwaxigqaxgxwdlotxdvxniafxndxmdoqaxvrbtxdpnxfdlaxgnxksijxtgmixsglaalmxtdnxsdxtdnxph which has xs in what look like sensible places for spaces. Here we can put them in:

rv ydp orha epzzoam wa igqa g wdlot dv niaf nd mdoqa vrbt dpn fdla gn ksij tgmi sglaalm tdn sd tdn ph

This is a substitution cipher and putting g as a (single letter word) gives you a way in. After some work you get:
IF YOU LIKE PUZZLES WE HAVE A WORLD OF THEM TO SOLVE FIND OUT MORE AT GCHQ DASH CAREERS DOT CO DOT UK

An advert for working at GCHQ. They've earned it I suppose.