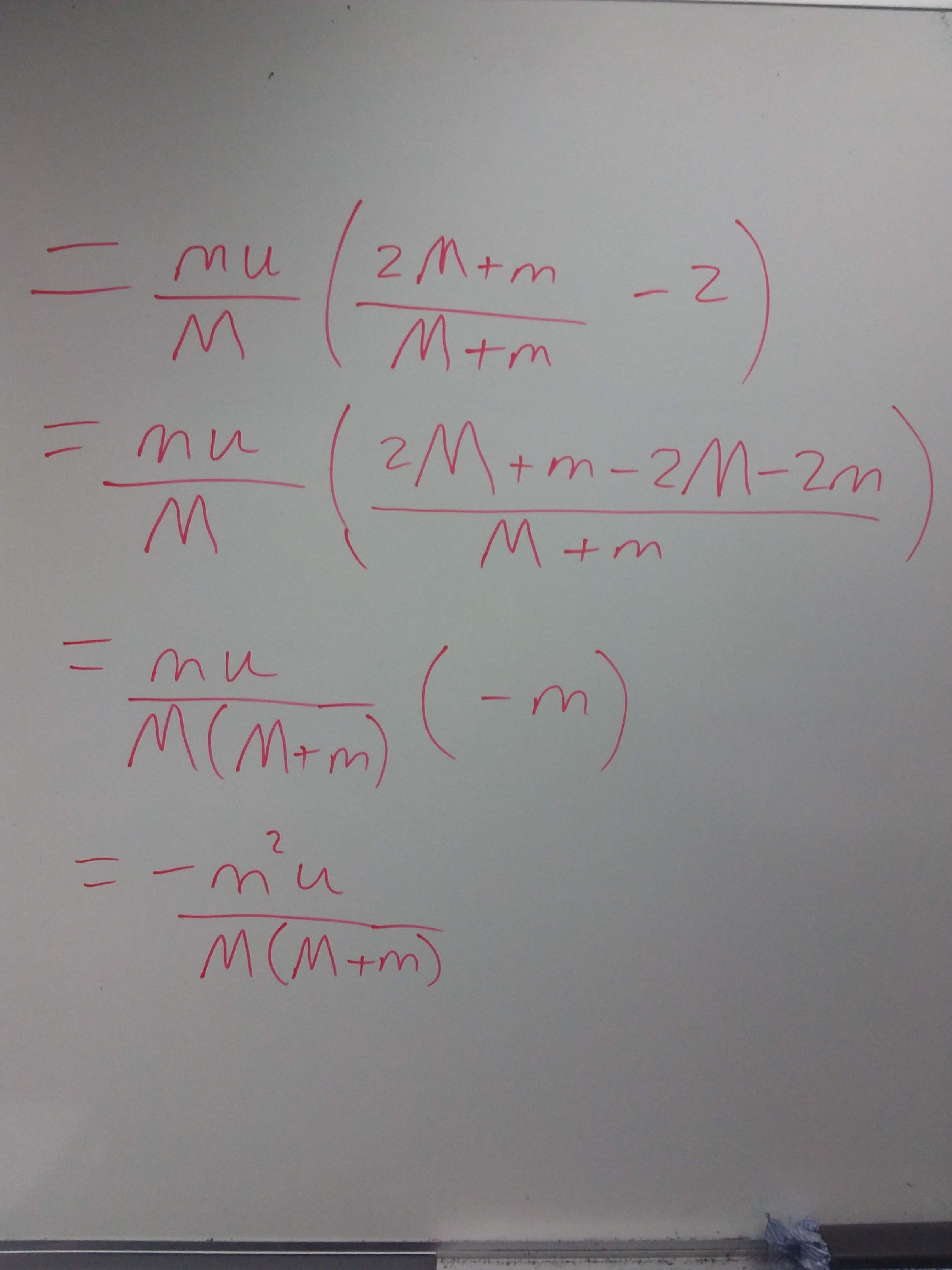Throwing Spaceboots

You are an astronaut and on a routine spacewalk you end up drifting away from your ship. Since there is no air (well about 4 atoms for every cubic metre, which is more or less the same as no air) in space you can't swim back to your ship. In fact, if you ended up just out of reach from your ship you would remain that way forever.

However, you are in luck because you realise you are wearing your extra chunky spaceboots which you can remove. If you throw a boot as hard as you can in the opposite direction to the one you want to travel in, then you can generate some velocity. Now here's the question: to maxamise the velocity and try to catch up with the ship should you throw one boot and then the other, or should you tie the shoelaces (these are trendy spaceboots) together and throw both boots at the same time?

Let's define some constants. Your initial speed is 0. Your mass is M and each of the boots can have mass m. Therefore the total mass of the system is M+2m. Let's assume you can throw a boot at velocity u.

The total momentum you can throw a boot at is therefore mu. This will provide you with the same momentum in the opposite direction since momentum is preserved, so you (together with the remaining boot) will have a momentum of mu. So the velocity boost that we get from throwing the first boot is:

Throwing the second boot we get a very similar boost of speed:

So overall we have a boost in velocity of:

Let's try the same thing but throwing both boots at the same time. Here is the velocity increase this time: 

To see which of these is a bigger increase in velocity we could take one away from the other and see if we get something positive or negative like this:

Which simplifies to:

This is negative which means that you gain more velocity by throwing them at the same time. I've delved into it a bit more and if you are forced to throw them one at a time then throwing the heaviest objects first gives you a bigger boost.