Hero of Alexandria
Sometimes known as Heron instead, Hero was a first century CE Greek inventor living in Egypt. I did a lot of the early work on phuematics including making an early plunger based pump that saw heavy use throughout the Roman Empire, but I want to focus on some of his more forward looking inventions, both mechanical and mathematical.
One of the ways many people have heard of Hero was as the inventor of the first vending machine. Like many of his mechanisms it was designed as a wonder for a temple and the product it dispensed was holy water. When a coin was inserted into a slot it would slowly roll down a plate which would tip a balance that opened up the source of water. Then the coin would roll off the end of the plate and the balance would reset closing off the pipe again. Thus you would get a consistent discrete amount of water for your money.
Another invention which was much more important was the aeolipile which would becomes the basis of steam engines. Here's a picture of it:
Heat was applied from the bottom with a fire. Inside the liquid water would expand and become steam. As it exits from the two bent output pipes the brass drum starts to turn. In later years this design would be adapted so that the turning motion could be used to power something, but Hero's design was used as another amusement for the temples.
While I'm on the subject, here's an interesting problem to think about. There are some sprinklers which have a spinning head shaped like a capital N where the output pipe comes up through the middle so that the water will flow out through the two bent pipes which makes the head turn. Imagine we put the nozzle under the water and switch it so that instead of spurting out water it socks it in. Which way around does the head spin? It isn't as simple as it sounds.
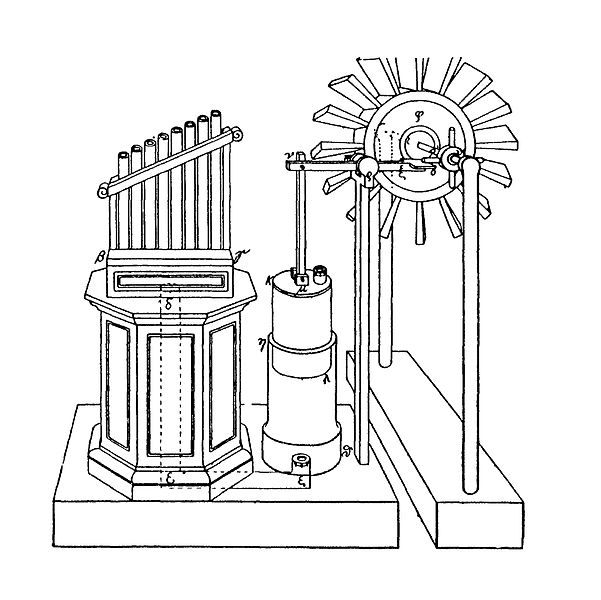
Back to Hero, he was the first person to use the wind to power a machine. This is the plan of a reconstruction: the windmill operated a pump which could provide the air for an organ. Later he invented mechanical plays which were entirely automated and reached up to 10 minutes in length.
To finish I want to mention two of his contributions to mathematics. The first was an iterative method to approximate the square root of a number. If you want to find the square root of S then you start with an approximation x0 and you use the iterative formula xn+1=(xn+s/xn)/2
This will give an arbitraily good approximation and is fairly fast for most small numbers and was the first formula of its type.
Secondly Hero had a formula for the area of a triangle just based on its three side lengths a, b and c. The half perimeter s is defined as (a+b+c)/2 and the area of the triangle = sqrt[s(s-a)(s-b)(s-c)]. It is a useful exercise to derive this formula from the cosine rule along with the generalised area of a triangle in terms of sin. Update: here's a later article I wrote going through this process.