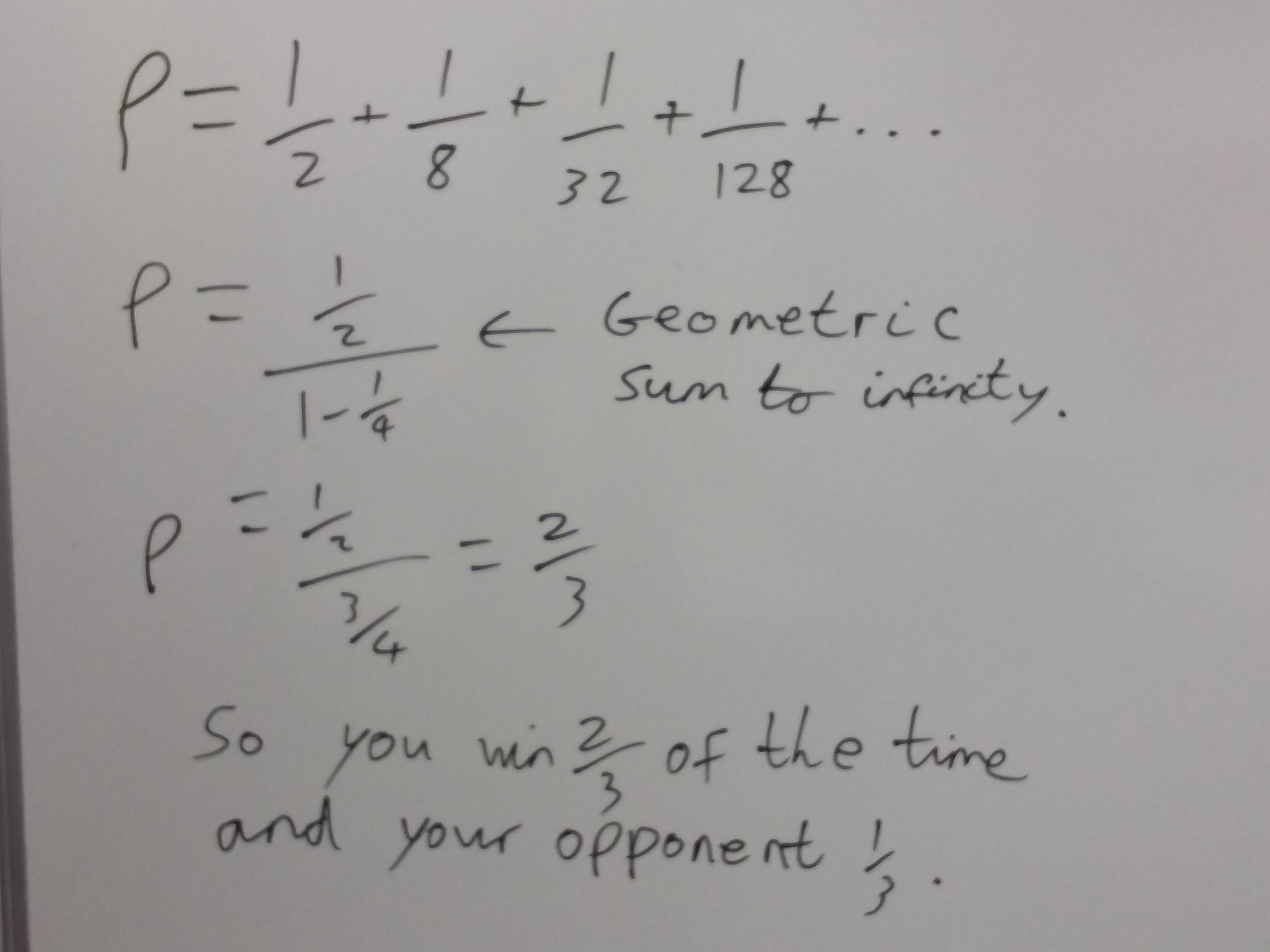Penney's Game — alaricstephen.com

We’ve already seen two examples of non-transitive games, with dice and with Rock Paper Scissors. I’m going to cover a different game, which is played with coins and is slightly less known.

Penney’s game is named after it’s inventor rather than the equipment used to play and is more of a trick than a fair game. You ask someone to name a sequence of 3 predictions for which side the coin will land on. You then pick a different sequence of 3 flips. A coin is flipped until the most recent 3 flips match someone’s prediction and that person is the winner.

For instance maybe your opponent picks HTT and you pick HHT. A coin is flipped and we have THHT at which point you have won. What is the best strategy for each player?

As with many of the games that I have covered recently it isn’t obvious to see that you can get more than a draw on average. For sequences of 3 outcomes there are only 8 possibilities and if you flip 3 coins each one should turn up 1/8th of the time.

Well let’s look at the easiest example to analyse in order to grasp what’s going on. Let’s try comparing their HHH with your THH. If the first 3 flips are all H then they will win, which will happen 1/8th of the time. But as soon as a T comes up at any point then Player 1 will need to go through 2 Heads in a row in order to get their HHH. But as soon as HH comes up Player 2 has won because there must have been a T proceeding the sequence. So any sequence other than an initial HHH will be a win for you eventually. With this setup you will win 7 out of 8 games.

How am I picking the correct sequence to work against theirs? There is a little trick: take the second symbol in their prediction and flip it- this is your 1st symbol. Then take their 1st and 2nd symbols and make them your 2nd and 3rd. For example (TH)H becomes T(TH). The Bold H has flipped to become our first T, then the bracketed TH has moved over to become our last two places.

We have seen why this strategy will work for HHH from above and TTT has exactly the same structure with Heads and Tails swapped around. However all of the other choices for Player 1 lead to more complicated analysis and all of them give slightly better winning probabilities for Player 1 than 1/8 although Player 2 always has an edge.

Below is my analysis of HHT versus THH:

The tree diagram shows the different paths the sequence can take. If the first move is a Tails then THH will always win because for the two Heads needed for HHT they will lose because the Red pattern will already be complete. This will happen half of the time.

If the first move is a Heads then we split into two possibilities. Heads leads to HHT winning and Tails leads to THH winning. So overall HHT will win 1/4 of the time, and THH will win 3/4.

I'm not going to analyse all of the combinations, but I wanted to show you one of the more complicated. Let's look at HTH versus HHT:

This one sometimes heads back to the start, explained below.

Ok, this is harder to get your head around. Since neither sequence seeks a Tail to start then flipping one just leaves us in exactly the some position as at the beginning. So we can just focus on the Heads branch to the left. After HH then the Red player definitely wins (1/2 the time). The other half we have HT. Half the time from here then the Black player will win (so 1/4 of the time overall), but the other half of the time we will have had HTT. Now since neither Player needs TT both have to restart waiting for their first Head again.

Possibly you can see that this gives HHT as probability of 2/3 compared with HTH as 1/3, but let's go into the recursive probability:

Breaking this down, the first 1/2 is just straight up getting to HH (after the first H has been down). + 1/2 ( 1/4 (which is the chance of getting back to the winning branch the second time through the loop) + 1/2 (1/4 + 1/2 (1/4 + ...))) The whole thing goes on recursively forever. But we can expand these all out like this:

If you remember your Geometric Sum to Infinity from C2 then this all works out quite neatly.

I haven't done HTT, but now you have seen this method you can follow through a similar thing yourself for it. I'll leave that up to you. Below I have a summing up picture of which pattern beats which and with which probabilities:

If you are feeling really ambitious, see if you can work out the rule for strings of four and what the optimal choices for each player are. This problem has been solved in general for strings of n.